En estos últimos años los algoritmos de Machine Learning (ML) han resuelto con éxito una amplia variedad de tareas alcanzando el state of the art en diversas áreas. Esto no solamente se debe al desarrollo de nuevos algoritmos (más potentes y más grandes), también en varias ocasiones, la selección de buenos hiperparámetros ha contribuido a esta conquista.

Optimización de hiperparámetros

Definimos como hiperparámetros a todos los parámetros de un modelo que no se actualizan durante el entrenamiento y que se utilizan para configurarlo. En la actualidad, una buena proporción de estos modelos tienen múltiples, diversos y complejos hiperparámetros que se deben ajustar para alcanzar un mejor rendimiento y esta tarea implica un gran desafío.

Conceptualmente, el ajuste de hiperparémetros se puede plantear como un problema de optimización, donde el objetivo es encontrar una configuración de hiperparámetros para un modelo determinado que nos permita obtener el mayor rendimiento posible sobre un conjunto de validación. Al método que se utiliza para resolver este tipo de problema se lo conoce como Hyperparameter Optimization (HPO) o Hyperparameter Tuning.

Matemáticamente, podemos formularlo del modo siguiente: Dado que el rendimiento que obtiene un modelo sobre un conjunto de validación puede ser modelado como una función f : X \(\to\) R de sus hiperparámetros x ∈ X (f puede ser cualquier función de error, por ejemplo el RMSE en un problema de regresión o el AUC Score para un problema de clasificación). El problema que deber resolver la HPO es encontrar x tal que:

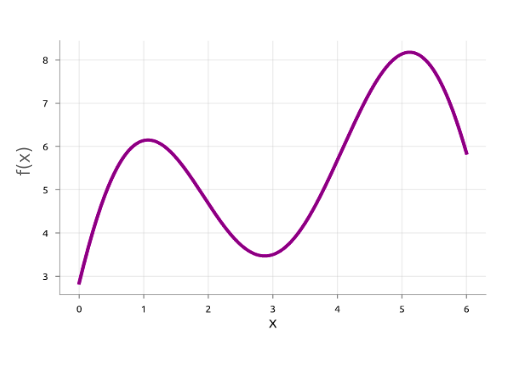
Hay varios puntos que este tipo de de optimización debe afrontar:

• En primer lugar, la evaluación de cada configuración es sumamente costosa, ya que implica entrenar un modelo y esto puede llevar horas o días.
• Como ya mencionamos, el espacio de búsqueda de hiperpámetros puede ser demasiado grande.
• Por otro lado, no se calculan gradientes, por lo tanto el método de optimización tendrá que buscar a ciegas dentro del espacio mencionado, o valerse de métodos que le permita generar búsquedas más inteligentes. Es por eso que a este tipo de optimización se la denomina como Black-Box Optimization.

Enfoques de HPO

Se han propuestos varios enfoques para abordar el problema de HPO. Este árticulo no está focalizado en profundizar a todos. Sin embargo, resumiremos brevemente los métodos más populares en efecto de tener un mayor entendimiento de cuales son las ventajas que nos proporciona Hyperband y cuales son las falencias que intentará suplir.

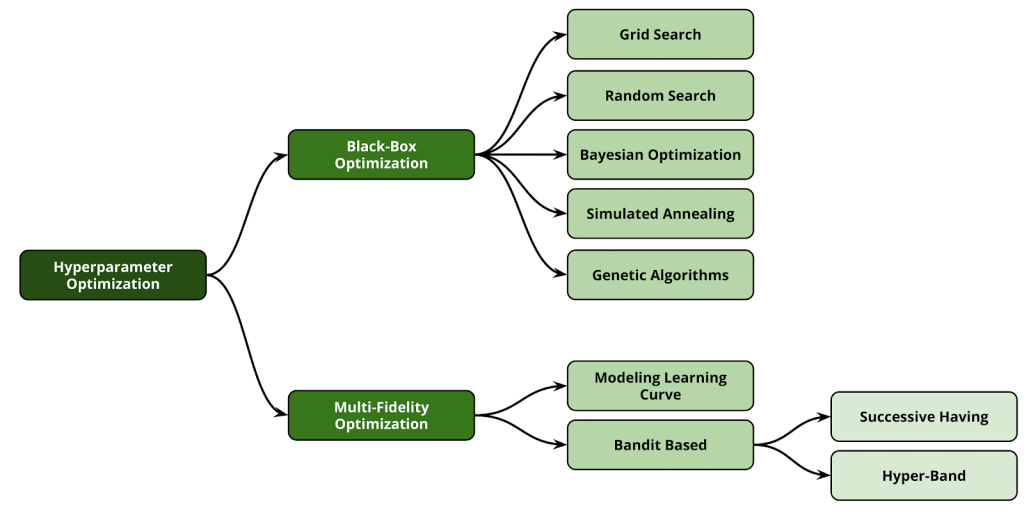
Grid Search/Random Search

Grid Search es uno de los enfoques más populares debido a su simplicidad al implementar. Este algoritmo actúa discretizando el espacio de búsqueda para poder generar todas las configuraciones posibles de hiperparametros. Luego, evalúa cada una de estas configuraciones, y al finalizar selecciona a la de mayor desempeño.

Este enfoque posee ciertas desventajas. Por un lado, el número de configuraciones a evaluar crecerá exponencialmente con respecto al número de hiperparámetros que se deban ajustar.

Por otra parte, supongamos que nuestro modelo solo tiene dos hiperparametros a configurar, uno es muy importante para su correcto funcionamiento y el otro no. Supongamos también que cada uno tiene 3 valores posibles y por ende nuestro espacio de búsqueda estará compuesto por 9 configuraciones diferentes en total.

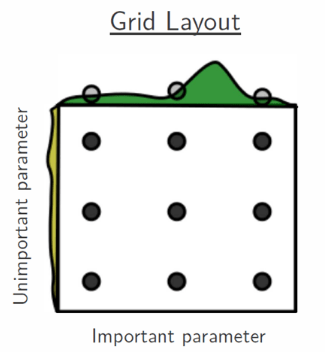
Como se puede observar en la figura anterior, el algoritmo no ha podido encontrar el mejor valor para el “hiperparámetro importante” luego de evaluar cada configuración debido al uso del espacio discretizado.

Random Search es una variante a Grid Search e intenta solventar la problemática anterior muestreando aleatoriamente configuraciones sin discretizar el espacio de búsqueda. Al no tener una condición de fin implícita la cantidad de configuraciones muestreadas a evaluar será escogida por nosotros.

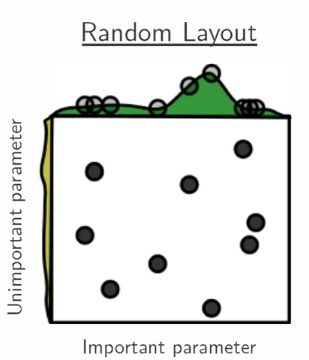
Este algoritmo también tiene la misma falencia respecto a la dimensionalidad del espacio de búsqueda, ya que a mayor espacio necesitará una mayor cantidad de muestreos para tener una mínima cobertura sobre este que asegure cierta aceptación.

Optimización Bayesiana

Tanto Grid Search como Random Search convergen eventualmente luego de un tiempo determinado. Pero en la práctica esto no es viable, ya que los recursos (tiempo y costos) de los cuales disponemos suelen ser limitados.

Dada estas restricciones, necesitaremos de algoritmos más inteligentes para buscar buenas configuraciones y abandonar por un momento las búsquedas a ciegas brindada por estos dos enfoques. Aquí es donde se nos presenta la Optimización Bayesiana (BO).

En esencia, la Optimización Bayesiana es un modelo de probabilidad que quiere aprender una función objetivo muy costosa basándose en observaciones previas. Tiene dos componentes principales: un modelo sustituto y una función de adquisición.

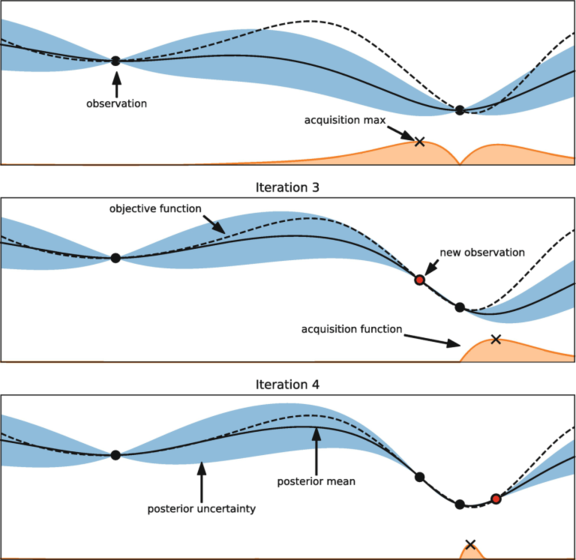
La figura anterior será un buen punto de partida para entender cómo es que BO trabaja. Como mencionamos inicialmente, nuestro objetivo es encontrar el punto que minimice la función objetivo f. Pero recordemos que desconocemos el valor real de esta.

Entonces, supongamos que inicialmente seleccionemos dos configuraciones para ser evaluadas (representadas por los puntos negros). A continuación, lo que BO tratará de hacer es ajustar un modelo sustituto (descrito por la línea negra continua junto a la sombreado azul de la incertidumbre de la estimación) para aproximar a f utilizando algún modelo probabilístico dada las configuraciones ya observadas.

Luego, la decisión de cuál será la siguiente configuración a evaluar sera tomada por la función de adquisición. Esta, intentará explorar aquellas zonas donde existe muy poca información y potencialmente podamos encontrarnos con buenas configuraciones.

Finalmente, la configuración seleccionada por la función de adquisición se agregará al conjunto de configuraciones ya evaluadas, y nuevamente se ajustará el modelo sustituto. Se iterará tantas veces como sea necesario, y al final seleccionaremos el punto que minimice la función aproximada.

Si bien BO funciona muy bien en este tipo de optimizaciones, tiene una desventaja que no podemos dejar pasar y es que no se pueden paralelizar los recursos debido a que el proceso es secuencial. Además, las variantes más clásicas de BO también tendrán problema con espacios de búsquedas de altas dimensiones.

Successive Halving

Antes de ir a nuestro tema en cuestión, debemos mencionar a su predecesor Successives Halving (SH).

La idea detrás del algoritmo deriva directamente de su nombre:

• Asignar uniformemente un presupuesto (Por ejemplo: tiempo de entrenamiento, número de epochs, etc.) a un conjunto de configuraciones de hiperparámetros muestreadas aleatoriamente.
• Evalúar el rendimiento de todas las configuraciones.
• Descartar la mitad menos prometedora cumplido un presupuesto determinado.
• Repetir hasta que quede sólo una configuración.

El objetivo de SH es asignar exponencialmente más recursos a configuraciones más prometedoras. Podemos observar que su funcionamiento es similar a Random Search, pero con la diferencia de que aplica early stopping, descartando aquellas configuraciones que peor desempeño estén obteniendo.

Desafortunadamente, también nos enfrentamos a un problema con este tipo de enfoque. SH requiere como entrada el número de configuraciones n a evaluar. Dado un presupuesto finito B, se asignan en promedio un presupuesto B/n entre todas las configuraciones. Sin embargo, para una B fija, no está claro a priori si deberíamos:

• (a) Considerar muchas configuraciones (n grande) con un tiempo promedio pequeño de entrenamiento; o
• (b) Considerar un pequeño número de configuraciones (n pequeña) con tiempos de entrenamiento en promedio más largos.

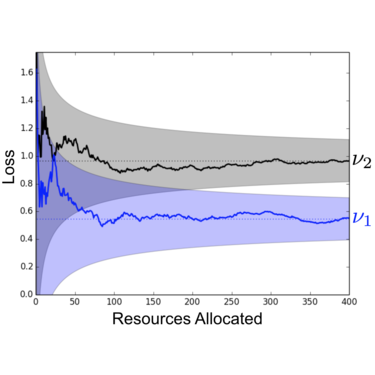
Utilizaremos un ejemplo para comprender mejor este balance. La figura anterior muestra los rendimientos obtenidos por dos configuraciones (v1 y v2) sobre un conjunto de validación en función de los presupuestos totales asignados.

Inicialmente, es muy difícil diferenciar una de la otra. Es más, podemos observar que v2 se estaría desempeñando mejor que v1. En este caso, si hubiésemos seleccionado un n grande, dado que el presupuesto asignado sería pequeño, probablemente hubiésemos descartado a v1 rápidamente.

Sin embargo, luego de un tiempo determinado, cuando el desempeño de ambas configuraciones se estabilizan, observamos que v1 ha sido en realidad la que mayor rendimiento ha obtenido.

A pesar de este obstáculo, SH agiliza considerablemente el tiempo de búsqueda de buenas configuraciones si es que se elige un n relativamente óptimo. Pero como pudimos observar, es una tarea sumamente difícil, convirtiendose esta decisión en otro hiperparámetro en cuestión.

Hyperband

Ahora sí, llegó el momento de Hyperband (HB). Al igual que su predecesor, HB pone el foco en acelerar el enfoque Random Search asignando un presupuesto de forma adaptativa, paralelizando los recursos y utilizando early stopping, poniendo así mayor atención en las configuraciones más prometedoras.

Esto le permite desempeñarse relativamente bien en problemas con espacios de alta dimensionalidad, y obtener así, un buen balance entre velocidad y performance. Aborda también el problema de “n versus B/n” que padece SH al considerar varios valores posibles de n para un presupuesto B fijamente preestablecido. En esencia, ejecuta Grid Search sobre varios posibles para n.

HB se observa en el Algoritmo 1. Asociado con cada valor de n habrá un presupuesto mínimo r que se asignará a todas las configuraciones antes de que se descarten algunas; un valor mayor de n corresponde a una r menor y, por lo tanto, una early stopping más agresivo (se descartaran más configuraciones en menor tiempo).

Hyperband tiene dos componentes principales:

• (1) El loop externo itera sobre diferentes valores de n y r. Es el responsable de “ejecutar GridSearch” para varios valores de n (líneas 1-2).
• (2) El loop interno que invoca a SH para valores fijos de n y r (líneas 3-9).

Este algoritmo requerirá de dos entradas:

• (1) R, la cantidad máxima de recurso que se puede asignar a una sola configuración.
• (2) η, una entrada que controla la proporción de configuraciones descartadas en cada ronda por SH.

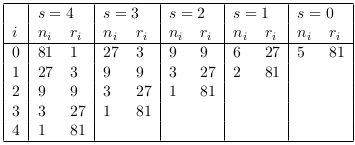
Tanto R como η determinarán los distintos valores para n y el presupuesto r que se utilizará en cada una de estas. HB iniciará con el valor más alto para n, maximizando así la exploración, y luego recorrerá los valores más pequeños, protegiendo así, a aquellas configuraciones que requieren de un mayor presupuesto.

Implementación de Hyperband

HB para poder funcionar requiere de las siguientes funciones:

• get_hyperparameter_configuration(n): una función que retorna un conjunto n de configuraciones muestreadas dada una distribución previamente definida.

• run_then_return_val_loss(t, r): una función que toma como entrada un conjunto de configuraciones t y el presupuesto r asignado a cada una de estas. Retorna el error sobre el conjunto de validación obtenido por cada configuración.

• top_k(configs, losses, k): una función que toma como entrada un conjunto de configuraciones y su performance. Retorna las k que mejor performance hayan obtenido.

Un ejemplo sencillo de como implementar Hyperband con Python puede observarse en el siguiente fragmento de código:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Importamos las dos funciones auxiliares que utilizaremos para HB
from problem import get_random_hyperparameter_configuration,run_then_return_val_loss

max_iter = 81  # Cantidad maxima de iteraciones o epoch por configuracion
eta = 3 # Definicion del downsampling rate (default=3)
logeta = lambda x: log(x)/log(eta)
s_max = int(logeta(max_iter))  # number of unique executions of Successive Halving (minus one)
B = (s_max+1)*max_iter  # total number of iterations (without reuse) per execution of Succesive Halving (n,r)

#### Comenzamos por el loop externo
for s in reversed(range(s_max+1)):
   n = int(ceil(int(B/max_iter/(s+1))*eta**s)) # Nro. inicial de configuraciones
   r = max_iter*eta**(-s) # Nro. inicial de configuraciones para evaluar una configuracion


   #### Bucle interno donde aplicamos Successive Halving with (n,r)
   T = [ get_random_hyperparameter_configuration() for i in range(n) ]
   for i in range(s+1):
       # Corremos para c/u de las n_i configuraciones r_i iterations y mantenemos las mejores n_i/eta
       n_i = n*eta**(-i)
       r_i = r*eta**(i)
       val_losses = [run_then_return_val_loss(num_iters=r_i, hyperparameters=t) for t in T]
       T = [T[i] for i in argsort(val_losses)[0:int(n_i/eta)]]

Podemos ver el ejemplo completo en el siguiente repositorio.

Vale la pena mencionar que existen varias implementaciones robustas para utilizar Hyperdband con todas las ventajas que nos ofrece. Dos sumamente recomendables son las desarrolladas por Ray Tune y HpBandSter.

Además, también disponemos de una implementación para utilizar con Sklearn.

Conclusiones

En la actualidad el correcto funcionamiento de un modelo de Machine Learning o Deep Learning depende en gran medida a sus hiperparámetros. Esta tarea no es para nada fácil, y es por eso, que muchas investigaciones han puesto el ojo en resolver este tipo de problemas. El enfoque a seleccionar dependerá mucho de nuestro problema en cuestión y del equilibrio que necesitemos entre velocidad y performance.

Referencias:

• A Tutorial on Bayesian Optimization, Frazier, 2018 (Paper) [LINK].

• Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization, Li et al., 2018 (Paper) [LINK].

• BOHB: Robust and Efficient Hyperparameter Optimization at Scale, Falkner et al., 2018 (Paper) [LINK].

• Automated Machine Learning Methods, Systems, Challenges, Capítulo 1 (Libro) [LINK].

• Exploring Bayesian Optimization (Artículo) [LINK].

Lecturas recomendadas:

• Bayesian Optimization Primer, SigOpt, 2015 (Paper) [LINK].

• Algorithms for Hyper-Parameter Optimization, Bergstra, 2014 (Paper) [LINK].

• A Conceptual Explanation of Bayesian Hyperparameter Optimization for Machine Learning (Artículo) [LINK].

• How to Implement Bayesian Optimization from Scratch in Python (Artículo) [LINK].

• Utilizing the HyperBand Algorithm for Hyperparameter Optimization (Artículo) [LINK].

• BOHB: Robust and efficient hyperparameter optimization at scale (Artículo) [LINK].

• Hyperband (Artículo) [LINK].