Feature Selection utilizando Algoritmos Genéticos y DEAP

Normalmente, debido a la considerable cantidad de datos de los cuales hoy disponemos, cuando desarrollamos modelos de Machine Learning nos encontramos ante un gran desafío que es el de la SELECCIÓN DE VARIABLES o CARACTERÍSTICAS. (FEATURE SELECTION) El objetivo es enfocarnos en aquellas variables importantes para el modelo, descartando de esta forma aquellas que no lo son. Así, minimizaremos los tiempos de desarrollo iterando en menor tiempo y obtendremos un feedback de nuestro entrenamiento mucho más veloz. Además, en muchos casos podríamos conseguir mejoras en la performance del modelo, ya que podríamos prescindir de variables que estén generando ruido y complejidad al modelo.
Contenido
Feature selection
Es el proceso de reducir el número de variables durante la construcción de un modelo. Muchas veces nos encontramos ante problemas donde intervienen grandes cantidades de datos y variables, esta situación nos puede acarrear ciertos inconvenientes:
- El entrenamiento se puede ralentizar considerablemente, requiriendo grandes cantidades de memoria y altos requerimientos de cómputos.
- La performance de algunos modelos podría verse afectada negativamente.
Ejecutar este paso manualmente, en el caso de que el número de variables sea significante sería impracticable. Es por eso existen diversas técnicas para realizarlo.
En este artículo no hablaremos de estas técnicas, pero te mostraré cómo utilizar Algoritmos Genéticos para efectuarlo.
Algoritmos Genéticos (GA)
Es un método evolutivo estocástico para la optimización de funciones basado en la teoría de la evolución expuesta por Charles Darwin.
Este opera sobre una población de cromosomas (individuos de la población o soluciones candidatas), los cuales típicamente son formulados como una cadena de bits. A estos bits se los conocen como genes y están representados con valores de 0s y 1s (encoding).
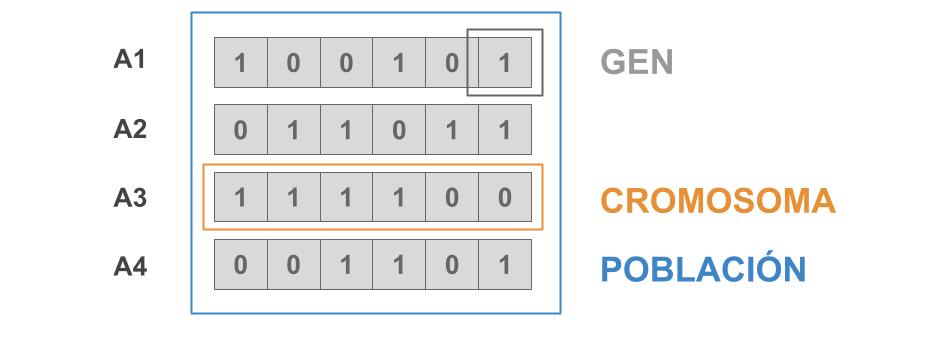
La idea es iterar generando sucesivas generaciones cada vez mejores a las anteriores. Esto se produce seleccionando a los mejores individuos de la población, de acuerdo a una función fitness, la cual evaluará y nos dará información sobre qué tan bueno es el individuo.
Luego combinaremos a estos individuos con otros, utilizando diferentes operadores para generar a los descendientes (o hijos). Por último, estos descendientes podrían someterse a una mutación, y estos conformarán la nueva generación.
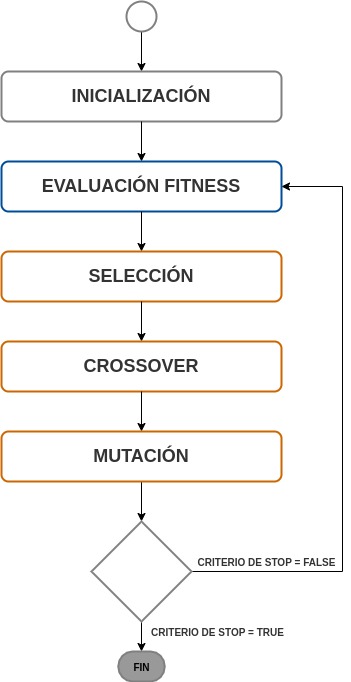
Un Algoritmo Genético Básico efectúa el siguiente flujo:
-
Inicialización: comenzamos generando de forma aleatoria una población de n cromosomas de longitud l (soluciones candidatas).
-
Calculamos la función fitness f(x) para cada cromosoma x en la población. Esta función evaluará la efectividad o aptitud de cada individuo.
-
Repetimos este paso por la cantidad de generaciones que deseemos crear:
-
Selección: Seleccionamos un par de cromosomas de la población actual. La probabilidad de selección estará dada por la función fitness. La selección se realiza con reemplazo, es decir, un cromosoma puede ser seleccionado más de una vez.
-
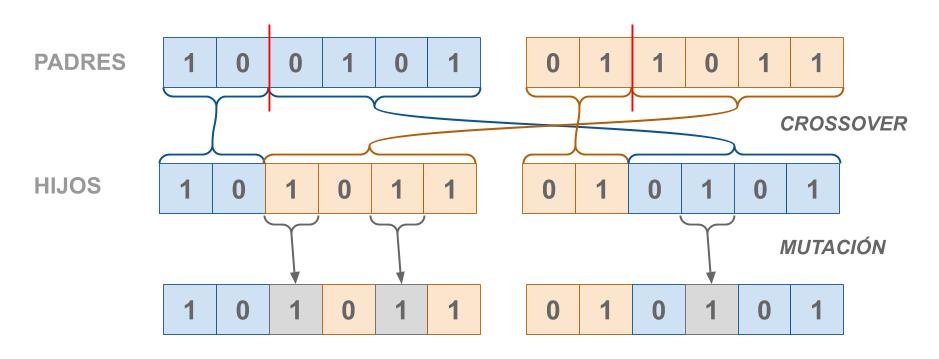
Crossover: Con una probabilidad \(\boldsymbol p_c\) combinamos un par de cromosomas seleccionados aleatoriamente y generamos dos descendientes.
-
Mutación: Mutamos a los dos descendientes del paso anterior en cada bit con una probabilidad \(\boldsymbol p_m\). Estos se convertirán en miembros de la nueva población.
-
-
Reemplazamos la actual población con la nueva población generada.
Intuición de la selección de variables con GA
Ahora que ya estamos familiarizados con ambos conceptos, veremos cómo estos trabajan en forma conjunta.
Matemáticamente, la selección de variables se puede plantear como un problema de optimización combinatoria. Donde las entradas serán las diferentes combinaciones de variables a evaluar, y la función objetivo será mejorar la performance de un modelo, tal vez reduciendo algún término de error. Es aquí donde aparecen los Algoritmos Genéticos para ayudarnos a resolver este tipo problema.
Podemos plantear la selección de variables con Algoritmos Genéticos de la siguiente forma. Supongamos que estamos trabajando en un problema de clasificación. El objetivo en este caso podría ser maximizar el F1 Score. Este será definido como nuestra función fitness. Esta función tomará como posibles soluciones un conjunto de individuos (distintas combinaciones de variables para entrenar el modelo), y evaluará su efectividad.
Estos individuos tomarán la forma de un vector de 0s y 1s. Su longitud será igual al número de variables del modelo y cada bit representará a cada una de estas variables. Si estamos en presencia de un 1, utilizaremos la variable correspondiente en esa posición para entrenar el modelo. Caso contrario no la consideramos.
Un ejemplo concreto sería el siguiente, tenemos a un individuo que será representado por el vector: [1, 0, 1, 0, 0, 0]. Este vector nos indica que vamos a evaluar la variable número 1 y la variable número 3.
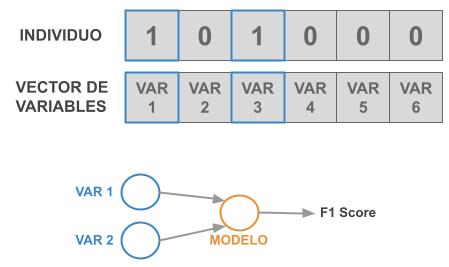
Cuando decimos que vamos a evaluar a este individuo, estamos diciendo que entrenaremos el modelo con estas variables y como salida obtendremos un score (F1 score), que nos indicará que tan bueno fue el desempeño de este conjunto de variables en el entrenamiento.
Por último, seguiremos el flujo visto en el punto anterior e iteramos tantas veces como nosotros definamos o hasta cumplir algún criterio para dejar de iterar. Al final del proceso tendremos a los mejores individuos (o soluciones) y seleccionaremos a el mejor. En nuestro caso será aquel con mayor F1 Score.
Implementación con DEAP
DEAP (Distributed Evolutionary Algorithms in Python) es un framework para cálculo evolutivo desarrollado en Python. Trabaja fácilmente con paralelización y multiprocesamiento. Además, nos brinda un conjunto de herramientas que rápidamente nos permite implementar y testear algoritmos genéticos.
Antes de comenzar con este tutorial, quiero comentarte que todo el código que veremos en este artículo estará disponible en mi repositorio de Github.
En primer lugar instalaremos las dependencias del proyecto. Utilizaremos los siguientes paquetes de Python:
Vale la pena destacar que dentro del repositorio se encuentra el README.md con los pasos necesarios para poder instalar todas las dependencias requeridas para utilizar el proyecto con sus respectivas versiones.
¡Ahora sí, manos a la obra! Lo primero que haremos es importar los módulos necesarios para que el código pueda funcionar.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np
import random
import matplotlib.pyplot as plt
from deap import algorithms
from deap import base
from deap import creator
from deap import tools
from sklearn import linear_model
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score, f1_score
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import StandardScaler
Dividiremos la implementación en 3 fases:
1. Generación del dataset y creación de la función de evaluación.
2. Instanciación del toolbox de DEAP y configuración del problema y los operadores.
3. Generación de un Algoritmo Genético Simple.
Primera fase: Generación del dataset y creación de la función de evaluación.
En este ejemplo trabajaremos con un problema de clasificación. Crearemos un dataset con la función make_classification y lo resolveremos con el modelo LogisticRegression.
1
2
3
4
5
6
7
8
9
10
11
# Definimos la cantidad de features a utilizar
n_features = 15
# Seteamos verbose en false
verbose = 0
# Generaramos el dataset
X, y = make_classification(n_samples=1000, n_features=n_features, n_classes=2, n_informative=4, n_redundant=1, n_repeated=2, random_state=1)
# Instanciamos el model
model = linear_model.LogisticRegression(solver='lbfgs', multi_class='auto')
Para implementar nuestra función fitness utilizaremos el modelo instanciado anteriormente y la métrica F1 score. Adicionalmente, usaremos crossvalidation para obtener una evaluación más robusta.
La función evaluate será la responsable de evaluar a cada individuo sirviéndose de la función calculate_fitness, la cual retornará el score correspondiente para ese individuo.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def calculate_fitness(model, x, y):
cv_set = np.repeat(-1.0, x.shape[0])
skf = StratifiedKFold(n_splits=5)
for train_index, test_index in skf.split(x, y):
x_train, x_test = x[train_index], x[test_index]
y_train, y_test = y[train_index], y[test_index]
if x_train.shape[0] != y_train.shape[0]:
raise Exception()
model.fit(x_train, y_train)
predicted_y = model.predict(x_test)
cv_set[test_index] = predicted_y
return f1_score(y,cv_set)
def evaluate(individual):
np_ind = np.asarray(individual)
if np.sum(np_ind) == 0:
fitness = 0.0
else:
feature_idx = np.where(np_ind == 1)[0]
fitness = calculate_fitness(
model, X[:, feature_idx], y
)
if verbose:
print("Individuo: {} Fitness Score: {} ".format(individual, fitness))
return (fitness,)
Segunda fase: Instanciación del toolbox de DEAP y configuración del problema y los operadores.
Para poder disponer del toolbox de DEAP tendremos que definir inicialmente que tipo de problemas afrontaremos (maximización o minimización). Indicaremos que es un problema de maximización asignando a weights la tupla (1.0).
1
2
3
4
creator.create("FeatureSelect", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FeatureSelect)
toolbox = base.Toolbox()
A continuación definiremos la estructura que tendrán nuestros individuos. Mencionamos al inicio que el individuo tiene que ser un vector de 1s y 0s, y su longitud tiene que ser igual al número de variables a utilizar.
Registrando attr_bool y luego utilizándolo en la configuración del individual cumpliremos con este objetivo. Seguidamente estableceremos que nuestra population estará conformada por estos.
1
2
3
4
5
toolbox.register("attr_bool", random.randint, 0, 1)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n_features)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
Por último, nos queda definir los operadores que emplearemos en este problema. Existen diferentes variantes para cada operador. Te dejo el siguiente link para que puedas obtener más información sobre esto: DEAP Operators.
1
2
3
4
toolbox.register("mate", tools.cxTwoPoint) # Crossover
toolbox.register("mutate", tools.mutFlipBit, indpb=0.1) # Mutacion
toolbox.register("select", tools.selTournament, tournsize=3) # Selecion
toolbox.register("evaluate", evaluate) # Evaluacion
Tercera fase: Generación de un Algoritmo Genético Simple.
Concluidas las dos fases anteriores, ya disponemos de las herramientas requeridas para poder implementar el algoritmo.
Previamente especificaremos algunas constantes, y una función auxiliar que nos facilitará la visualización de las estadísticas en la evaluación de cada generación.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
N_POP = 100 # Tamaño de la población
CXPB = 0.5 # Probabilidad de crossover
MUTPB = 0.2 # Probabilidad de mutación
NGEN = 10 # Cantidad de generaciones
print(
"Tamaño población: {}\nProbabilidad de crossover: {}\nProbabilida de mutación: {}\nGeneraciones totales: {}".format(
N_POP, CXPB, MUTPB, NGEN
)
)
# Función para generar salidas con estadisticas de cada generacion
def build_stats(gen, pop, fits):
record = {}
length = len(pop)
mean = sum(fits) / length
sum2 = sum(x * x for x in fits)
std = abs(sum2 / length - mean ** 2) ** 0.5
record['gen'] = gen + 1
record['min'] = min(fits)
record['max'] = max(fits)
record['avg'] = mean
record['std'] = std
print(" Min {} Max {} Avg {} Std {}".format(min(fits), max(fits), mean, std))
return record
Ahora sí, pasaremos a la implementación del Algoritmo Genético Simple. Seguiremos el flujo visto en la sección de Algoritmos Genéticos.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# Inicializamos a la poblacion
pop = toolbox.population(N_POP)
print("Evaluamos a los individuos inicializados.......")
fitnesses = list(map(toolbox.evaluate, pop))
# Asignamos a los inviduos el score del paso anterior
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
fitness_in_generation = {} # Variable auxiliar para generar el reporte
stats_records = [] # Variable auxiliar para generar el reporte
print("-- GENERACIÓN 0 --")
stats_records.append(build_stats(-1, pop, fitnesses[0]))
for g in range(NGEN):
print("-- GENERACIÓN {} --".format(g + 1))
# Seleccionamos a la siguiente generacion de individuos
offspring = toolbox.select(pop, len(pop))
# Clonamos a los invidiuos seleccionados
offspring = list(map(toolbox.clone, offspring))
# Aplicamos crossover y mutacion a los inviduos seleccionados
for child1, child2 in zip(offspring[::2], offspring[1::2]):
if random.random() < CXPB:
toolbox.mate(child1, child2)
del child1.fitness.values
del child2.fitness.values
for mutant in offspring:
if random.random() < MUTPB:
toolbox.mutate(mutant)
del mutant.fitness.values
# Evaluamos a los individuos con una fitness invalida
weak_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = list(map(toolbox.evaluate, weak_ind))
for ind, fit in zip(weak_ind, fitnesses):
ind.fitness.values = fit
print("Individuos evaluados: {}".format(len(weak_ind)))
# Reemplazamos a la poblacion completamente por los nuevos descendientes
pop[:] = offspring
# Mostramos las salidas de la estadisticas de la generacion actual
fits = [ind.fitness.values[0] for ind in pop]
stats_records.append(build_stats(g, pop, fits))
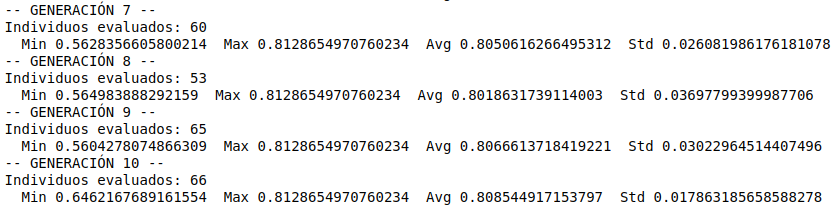
Para poder simplificar un poco el reporte anterior, te dejaré una visualización con la performance de cada generación.
1
2
3
4
5
6
# Ploteamos el AVG por generacion
plt.figure(figsize=(10,8))
front = np.array([(c['gen'], c['avg']) for c in stats_records])
plt.plot(front[:,0][1:], front[:,1][1:], "-bo", c="b")
plt.axis("tight")
plt.show()
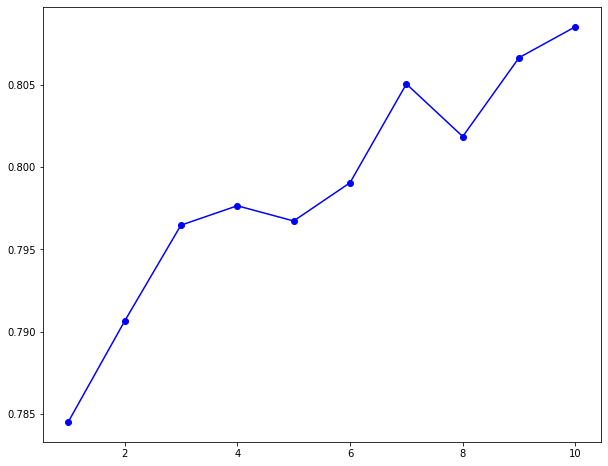
Claramente podemos notar que mientras vamos “avanzando en la evolución” el score promedio de todos los individuos se va incrementando. Podemos concluir que cada generación está mejorando a la generación anterior, y en consecuencia se están generando mejores individuos (soluciones).
Cabe destacar que estamos utilizando un algoritmo simple. Pero existen mucho más. Para que no tengas que implementarlos desde 0 DEAP nos provee varios algoritmos ya construidos. Te recomiendo nuevamente que vayas a mi repositorio de Github donde podrás ver un ejemplo.
Para finalizar, cuando terminemos de evaluar a los individuos de la última generación, procederemos a seleccionar al mejor individuo, es decir, la mejor combinación de variables que maximice el F1 score.
1
2
3
4
best_solution = tools.selBest(pop, 1)[0]
print(
"El mejor individuo es: \n{}, con un F1 Score de {}".format(best_solution, best_solution.fitness.values)
)

Conclusiones
La selección de variables es uno de los grandes desafíos que enfrentamos durante la construcción de un modelo. Existe una amplia cantidad de métodos a utilizar, los cuales ofrecen sus ventajas y desventajas. Los Algoritmos Genéticos son una alternativa más a utilizar. Son fáciles de implementar y de entender.
Definir que método deberíamos emplear es un desafío en sí mismo. Un factor clave será entender cuáles son nuestras necesidades. Solo así cumpliremos con nuestros objetivos.
Referencias:
 No te pierdas los próximos posteos, suscríbete
No te pierdas los próximos posteos, suscríbete